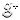What does it mean for a machine to make an utterance? Friedrich Kittler famously probed this question with reference to, among other things, Kruesi’s talking machine, the design of the Zilog Z80 microprocessor, and the Colossus and Enigma machines.1 More recently, in the years immediately following the Snowden disclosures (2013-), the use of encryption technology has increased to a point where more of our digital communications are encrypted than not.2 Today, the majority of us write in ways that we cannot read or ever hope to comprehend; by default, writing is transposed into ineffable, encrypted tunnels of “secure” information. In one way or another, machines speak for us.
In this article, I sketch an archeology of machine translation, showing how its origins are to be found in the invention of cryptanalysis, or “code-breaking.” I trace this archeology through the cryptanalysis and translation practices of medieval Arabic scholars, the machine translation efforts within Renaissance and Early Modern universal language planning, and the recently declassified cryptanalysis techniques developed by NSA chief cryptanalyst William Friedman. These histories then find their apotheosis in Warren Weaver’s influential “Translation” memorandum. In this short and influential memorandum, Weaver developed a “cryptographic-translation” idea, drawing on his knowledge of World War II code breaking to launch the modern field of machine translation. Together, these histories reveal some of the ways that various machineries were developed to “crack” unknown text, be it a foreign language or ciphertext. As such, this history also points to a deeper, ontological relationship between language and cryptology.
This history is framed by the longstanding (and notorious) tension between rationalist and empiricist approaches to language. Conventionally and controversially, rationalist approaches to language sometimes suppose a mentalist account of the sign, a grammar common to all languages, and the human power of intuition. On the other hand, and no less controversially, empiricist approaches to language hold that knowledge is dependent on sense experience, and that language is therefore learned. In the histories of machine translation and cryptanalysis, this tension also persists, configured as rationalist-universal and empiricist-statistical. Rationalist-universal approaches use machinery to configure common and foundational aspects of language (its deep structure), whereas empiricist-statistical approaches use machinery to calculate or compute its letters and relationships (its surface). This tension between theories of language, thought, and the practice of language in use is maintained throughout the histories of machine translation and cryptanalysis.
Cryptology is the study of cryptography and cryptanalysis. Cryptography and cryptanalysis, however, are ontologically distinct. On this point I am strict and precise. Cryptography is comprised of encryption and decryption. Encryption and decryption are the deterministic processes of substituting, ordering, and permuting discrete inscriptions.3 Decryption is the precise reversal of encryption – a way of stepping backwards, from ciphertext to plaintext. Cryptanalysis, on the other hand, is a form of intuitive guesswork that reveals plaintext from ciphertext, and therefore always admits the possibility of error (even when rationalized, systematized, or mechanized).
Unlike most literature on the subject, which often uncritically blurs the distinctions between cryptanalysis and decryption, I maintain the ontological division, even if in practice the terminology and methods are often blurred. Critically, it is cryptanalysis that is aligned with and occupies the same complex ontological and technological array of the techniques of machine translation. So, in tracing these historical and ontological distinctions, I conclude that Warren Weaver’s proposal for a “cryptographic-translation” solution for machine translation should rather be called a “cryptanalysis-translation” solution, as it draws on the history and ontology of cryptanalysis (and not cryptography). Nonetheless, despite occasional terminological and conceptual mistakes, the history and techniques of machine translation evolve from and are codetermined by the history and techniques of cryptanalysis.
Early History of the Codetermination of Cryptanalysis and Machine Translation
The history of machine translation is commonly thought to originate with the early language planners in the sixteenth and seventeenth centuries, who were interested in using cryptological technologies for machine translation.4 In this tradition, the earliest machines that were built specifically for translation were also often conceived by their designers as machines for cryptology, such as with Georges Artsrouni’s 1933 machine for translation.5 This history continues after the Second World War with Warren Weaver’s return to the connection between cryptology and machine translation.6 Weaver described a plan to develop a “cryptographic-translation” technique, arguing that by using techniques of cryptanalysis first developed in the War, he would be able to perform machine translation.7 Weaver’s idea would ultimately prove influential, and through its development by Andrew D. Booth, Richard Richens, Yehoshua Bar-Hillel, among others, and alongside development by modern corporations and universities, the field of modern machine translation was born out of and alongside cryptology.
I complicate and extend this narrative of machine translation by tracing it through a longer history of cryptanalysis. This history begins before the Western precursors in the sixteenth and seventeenth centuries, and distinguishes itself from these latter efforts, which were largely cryptographic (involving encryption/decryption), and not necessarily cryptanalytic.
Arabic Origins of Cryptanalysis and Systematic Language Translation
In the most influential book on the history of cryptology, David Kahn argued that “cryptology was born among the Arabs,” in that “they were the first to discover and write down the methods of cryptanalysis.”8 His assessment was prescient, and has proven accurate over the years, even after the discovery of a cache of important new manuscripts. In discovering the methods of cryptanalysis, medieval Arabic scholars9 used this knowledge to inform their practice of translation, and used their knowledge of translation to aid their practice of cryptanalysis.
The invention of cryptanalysis by Arabic scholars was no accident. During the so-called Islamic “Golden Age” (a somewhat problematic catch-all term, denoting a period of intellectual vibrancy from roughly the eighth to thirteenth centuries of the common era), Arabic scholars possessed the suitable intellectual and political skills and the necessary motivations for the development of cryptanalysis – which are also, it turns out, the same skills and motivations necessary for systematic language translation (systematic language translation is distinguished from “craft” or intuitive translation in that it uses a rigorous and formalized procedure). Specifically, Arabic scholars during this era were highly skilled in mathematics, had a well-developed political state, and had a sophisticated understanding of linguistics (both Arabic and other).
The invention of a practical numeral notation and the concept of zero (both of which the West later adopted) were critical features on the path to robust statistical mathematical knowledge. Armed with a knowledge of statistics and an ability to calculate large and complex numbers Arabic scholars were able to derive empirical letter frequency counts from texts, a necessary skill for cryptanalysis.
Arabic scholars also enjoyed a well-developed and well-funded state administration (the caliphate), which included both a rich academic tradition and a proficient bureaucracy. The needs of a strong state administration provided many reasons and motivations for the practical development of cryptography and cryptanalysis – bureaucratic skills associated with a highly literate state environment for use in statecraft and diplomacy.10
Several factors contributed to success and proficiency in cryptanalysis, including proficiency in linguistics that developed as part of a critical apparatus of Quranic interpretation, the production of complex literatures (including poetry and prose), and a large, state-sponsored translation effort (its zenith was the Graeco-Arabic translation movement of the ‘Abbāsid caliphate).11
The development of sophisticated skills in text analysis was not just a product of state motivations. Many Arabic scholars of this era believed that language was sacred, powerful, and, in many cases, coded (a view then shared by scholars in the West).12 Since language was often considered coded, textual analysis was a necessary skill to reveal “hidden” meanings. For example, ibn Khaldun (1332-1406 CE) believed that words were veils, which concealed the links between thought and understanding.13 In effect, humans could not escape the challenges wrought by language (an identical issue in the West became known as the “Babel problem”).14 However, according to ibn Khaldun, humankind’s “greatest power and gift” was communication – roughly, the ability to lift the veil of language, given the right tools.15 These tools were associated with cryptanalysis and translation.
In the 1980s, a number of new cryptology manuscripts were discovered in the as-Sulaymaniyya Library in Istanbul, which have corroborated Kahn’s earlier assessment that it was Arabic scholars who had invented cryptanalysis.16 Among these manuscripts was al-Kindi’s Risala fi ‘istikhrag al-mu‘amma,17 written in the ninth century – over five hundred years before al-Qalqasandi’s work (which Kahn had referenced earlier), and long before Leon Battista Alberti’s work that introduced the systematic study of cryptography and cryptanalysis to the West.18 Al-Kindi’s work was deeply influential for the Arabic cryptologists that followed, often drawing their inspiration or substance from it.
These new manuscripts demonstrated that Arabic scholars had a detailed and highly developed set of terminologies with precise analytical distinctions for the field of cryptology. For instance, Arabic scholars distinguished between encryption (“at-ta‘miya”)19 and cryptanalysis (“at-targama” or “istihrag al-mu‘amma”), although sometimes the latter stood in for the entire field (what we now call cryptology). Similarly, Arabic scholars had words for most modern distinctions: plaintext, ciphertext, nulls, code, keys, steganography, n-grams, and so on.20 Cryptanalysis (istihrag al-mu‘amma) was considered the process of converting ciphertext into plaintext, which was sometimes also called “interpretation” (at-targama),21 and, importantly, also meant “translation.” The processes of encryption and decryption, however, were usually understood as distinct from cryptanalysis, and instead involved the reordering and substitution of letters.
In the Risala fi ‘istikhrag al-mu‘amma, al-Kindi revealed a deep and sophisticated understanding of language and statistics. Al-Kindi recommended that his readers use his statistical techniques only when the text was of “sufficient” or statistically-significant, size. Al-Kindi also detailed several cryptanalysis techniques based on letter frequency analysis, which were not only effective for revealing a probable plaintext from ciphertext but could also help determine the language in which any given text might be “encoded” (later, we will see echoes of this same technique and the underlying theory of language in Weaver’s proposals). It was through al-Kindi’s study of linguistics that he derived a knowledge of patterns and features within and across languages.
One such approach included the analysis of vowel-consonant ratios and letter-frequency stylometrics. Al-Kindi discovered that the vowel-consonant ratio of a given text is highly dependent on the specific language. Al-Kindi used the example of Latin when describing the ways that “certain languages… [have] vowels… greater in number than some other vowels, while non-vowels [i.e., consonants] may be frequent or scarce according to their usage in each language.”22 Aware of this technique’s possibilities, al-Kindi suggested that his approach worked best when comparing corpora of the same genre, since, he noted, genres have different letter distributions.23 In assessing the history of this technique, Bernard Ycart claims that it was al-Kindi’s early explorations of vowel-consonant ratios that anticipated computational linguistics, including questions of authorship attribution and stylometrics.24
When it came to cryptanalysis, al-Kindi developed three principal techniques, drawn from both the empiricist-statistical and rationalist-universal approaches to language. The first and perhaps most powerful of al-Kindi’s techniques of cryptanalysis used letter frequencies. Al-Kindi called this process “the quantitative [kammiyya] expedients of letters,” which worked by first “determining the most frequently occurring letters,”25 and then tabulating and comparing these against normal (plaintext corpora) distributions. To aid the reader, al-Kindi produced tables of letter frequencies for normal distributions in Arabic – the first ever such exercise, which would eventually become a vital practice for early statistics (Fig. 1).26 Armed with normal and ciphertext letter distributions, to cryptanalyse a ciphertext, al-Kindi wrote, “we mark the most frequent letter ‘first’, the second most frequent ‘second’,” and so on; then, in the letter distribution for our plaintext corpora we search “for the most frequent symbol… and regard it as being the same letter we have marked ‘first’… .”27 That is, plaintext and ciphertext letter frequency distributions were compared to see if a transposition through simple encryption had occurred, and then, working backwards, the plaintext could be determined from the ciphertext.
With this technique, al-Kindi was able to compare statistical probabilities across corpora, and to move across textual boundaries – between plaintext and ciphertext, and source and target languages. This technique could be used for cryptanalysis and determining the underlying language of a ciphertext.
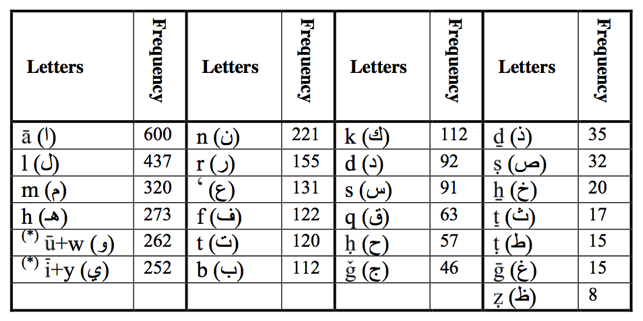
Fig. 1: Reproduction of al-Kindi’s letter frequency table.28
Al-Kindi’s second technique was based on presumed underlying linguistic rules, more typically associated with a rationalist-universal approach to text analysis. Al-Kindi investigated morphology and word derivations as part of the science of the “laws of single words,” which, as a counterpart to the first method, was used for “qualitative [kayfiyya] expedients.” On the basis of these laws, al-Kindi described “combinable” and “non-combinable” letters, and determined their valid orders and positions.29 These morphological rules, al-Kindi argued, reduced the number of possible valid letter positions, which could also be combined with letter frequency statistics. Later, ibn ‘Adlan (1187-1268 CE) further developed al-Kindi’s approach, analyzing valid n-gram combinations, such as bigrams and trigrams, compared against a dictionary of words used to determine which combinations of letters form actual words.30
The third technique of cryptanalysis described by al-Kindi was based on the semantic properties of actual texts – called the “probable word” method. Al-Kindi noted how common words or phrases, such as the traditional opening for Islamic works, “In the name of God, the Compassionate, the Merciful,” could be used “as a guide throughout the cryptogram.”31 That is, if a cryptanalyst could find ciphertext corresponding to certain common or probable words or phrases, guesses could be made to reveal the corresponding plaintext letters, which may also reveal a key or common substitution used throughout. Al-Kindi also recommended that the cryptanalyst pay attention to the fact that genres and styles may have unique phrases and probable words, which could be used for cryptanalysis.32
Al-Kindi’s techniques appear to have had limited impact on Western scholarship. Cryptanalysis in the West was largely conducted through state and Papal offices, called “Black Chambers.” These Black Chambers were efficient organs of state cryptanalysis, but contributed little to the techniques of art. However, by the thirteenth century, as the bloom of the Islamic “Golden Age” began to wither (traditionally attributed to the collapse of the ‘Abbāsid caliphate from Mongol attacks), Western cryptanalysis showed slow improvement. Alberti’s De Cifris (1466) was later an important work in the West, and foreshadowed the development of philosophical and “perfect” language planners, alongside their numerous calculating and “computing” machines, developed in some cases to automate translation.33 This tendency to design, plan, and program languages was an important precursor to intellectual currents we now associate with figures from early computing, including Weaver and Claude Shannon, who were critical to the development of key theories of information and the tools of modern information processing.34
Western Origins of Early Machine Translation
Through the sixteenth and seventeenth centuries, Western scientists developed innumerous techniques and technologies for transforming and manipulating text, largely in attempt to discover or invent universal, perfect, and philosophical languages.35 These “universal language planners” developed systems of textual manipulation to work across written languages and various encipherments or encodings (with only a few exceptions, universal language planners developed “pasigraphies,” or purely textual systems, rather than spoken language systems).36
The translation systems developed by universal language planners, however, typically used techniques of encryption and decryption rather than cryptanalysis. Since these systems drew on different sets of techniques and ontologies, their ability to manipulate language looks rather different, and in some ways quite rudimentary, in comparison to the work of al-Kindi. As a form of early machine translation, these machines typically did little more than word-for-word dictionary substitutions, with predictably lackluster results. However, where al-Kindi might have excelled at providing a rich set of statistical, morphological, and semantic tools for use in translation, the universal language planners made strides in automation.
One of the most common and efficient systems to aid translation was the multilingual code list, which took inspiration from the code lists found in cryptology. One such system was developed by Johannes Trithemius, who, in his cryptography manual Steganographia, developed code lists for learning Latin. Athanasius Kircher then expanded Trithemius’ idea for his own universal language system, the Polygraphia nova. In this work, Kircher proposed a system for translation that reduced text to its shared, essential aspects across languages.37 Translating using Kircher’s system meant first locating an object word in a special dictionary Kircher had developed. This word was transformed, or reconstructed, by looking up its semantic base and adding special symbols for tense, mood, verb, number, and declension. The resulting word, a semantic universal coded by Kircher’s system, could then be translated into a target language, if desired, by continuing the process with a dictionary developed for the target language in question. Of course, according to Kircher, translation into a target language was optional, since he envisioned that the universal, coded version might function as a suitable language itself.
Among scores of devices Kircher developed for “calculating” arithmetic, geometry, occult symbolisms, musical scores, and enciphering,38 Kircher created several wooden “computers” for retrieving and permuting codes. The Arca Glottotactica made word-for-word substitutions by moving wooden slats and panels, in effect automating the translation process. Like the Polygraphia nova, the device accommodated grammatical features, such as plurals, tenses, and cases.39
Many other universal language planners of this era also developed translation techniques and machines drawn from the field of cryptology. For example, Francis Lodwick and Cave Beck each wrote books on translation that were informed by the cryptographic work of Trithemius and John Wilkins. Wilkins himself published an important universal language scheme, the Essay Towards a Real Character and a Philosophical Language, which was based on his earlier cryptography manual, Mercury: A Secret and Swift Messenger.40 Johann Joachim Becher published a Latin vocabulary with a coded, numeric notation that, a year after its initial publication in 1661, was republished and publicized as a program for translation.41 Also in 1661, Becher published his Character, which included methods for “translating” Arabic numerals into lines and dots, a kind of “encipherment” that he thought deployed a more universal form of notation.42 Francis Bacon’s scientific work, with its universal aspirations, was also directly influenced by his work in cryptology (specifically, his binary-encoded “bi-literal” cipher). Bacon developed “Real Characters” that he thought ensured direct correspondences between words and things, and by extension, constituted the essential, rational unification of languages.43
Gottfried Wilhelm von Leibniz’s interest in universal languages marked the beginning of the end for early language planning, and represented a point of transition between early efforts at regularizing and automating translation manually, such as with Kircher’s Polygraphia nova, and later genuinely computational approaches to translation.44 The first of Leibniz’s analytical and calculation machines was his invention of a stepped reckoner in 1673. Although the stepped reckoner could only perform simple arithmetic (it added multiplication to an earlier variant designed by Blaise Pascal), Leibniz envisioned (but never finished) a device for transforming many things, including language and cryptography.45
Thus emerged one version of what we later called the “computers” of Babbage and Lovelace, Boole, Turing, and von Neumann. While these machines are celebrated for their proficiency in numeric calculation, we ought to also remember the ways that language translation and cryptology informed and codetermined their history.
Early Twentieth Century Cryptanalysis and Translation
In 2005, the US National Security Agency declassified a trove of materials written by its celebrated chief cryptologist, William Friedman (1891–1969).46 Contained in these materials were Friedman’s groundbreaking cryptanalysis manual, “The Index of Coincidence” (first proposed in 1920, published internally in 1922),47 and a series of previously classified training manuals detailing and rationalizing existing cryptanalysis techniques. These techniques, especially as described in the early “Index of Coincidence” publication, are enormously important to the history of cryptology; David Kahn called the “Index of Coincidence” the “most important single publication in cryptography.”48
Below, I focus on the series of training manuals entitled Military Cryptanalysis. The techniques described in the series cannot be considered “cutting edge” for the time, as they are simpler in design than the “Index of Coincidence” technique.49 Despite their relative simplicity, the training manuals offer insight into the kinds of cryptanalysis techniques that Warren Weaver (not a cryptographer or cryptanalyst) might have been exposed to during his bureaucratic and scientific activities.
Consulting Friedman’s work helps me highlight two important points: 1) the methods and ontology of cryptanalysis are closely aligned with systematic language translation; and 2) the techniques of cryptanalysis available in the early twentieth century reflect a long history from medieval Arabic cryptanalysis to Weaver’s “cryptographic-translation” idea. Given this trajectory, the sense of cryptanalysis that emerged in the Military Cryptanalysis series presented a surprising conjunction with machine translation, which we might see as a potential inspiration for Weaver’s subsequent idea, or at least a vindication of it.
Friedman’s Military Cryptanalysis series contains four volumes of ascending difficulty and utility, published between 1938 and 1941. The first volume lays the groundwork, starting with simple monoalphabetic ciphers and the letter frequency distribution method of cryptanalysis, which is identical in its essential aspects to al-Kindi’s earlier work. The latter volumes tackle newer ciphers and more advanced methods of cryptanalysis, covering techniques that developed after al-Kindi, such as polyalphabetic encryption, which was unknown to the Arabic cryptologists (polyalphabetic encryption was invented by Alberti in his 1466 manuscript, De Cifris).
Friedman described four basic operations of cryptanalysis, which were: 1) the determination of the language employed in the plaintext, 2) the determination of the general system of cryptography employed, 3) the reconstruction of a key or code book, and 4) the reconstruction or establishment of the plaintext.50
To determine the language of the plaintext, Friedman first suggested that the cryptanalyst might make an educated guess, based on prior knowledge about the origins of the ciphertext message. But, in more complex cases, the sender may have used an unexpected language as subterfuge, which would frustrate guesses (for example, the Germans would occasionally write in English during the First World War).51 A more systematic approach, Friedman offered, was to exploit the fact that “the language employed is found in the nature and composition of the cryptographic text itself.”52 For instance, Friedman noted that certain languages did not contain or rarely used certain letters (Friedman cited the lack of letters K and W for Spanish, echoing al-Kindi’s observation that the letter S occurred frequently in Latin). Friedman also described other unique linguistic features that might help the cryptanalyst determine the underlying language, such as special bigraphs (CH in German), or regionally-specific eccentricities (Japanese Morse code contained many unique combinations).53 Knowing these special characteristics of language, Friedman stressed, was a critical aspect of successful cryptanalysis.
Friedman suggested that in some cases cryptanalysis could even proceed without knowing the underlying language. Friedman called this “frequency studies.” But even in these cases, there was a role for translators (although, perhaps not the usual one). Friedman described “analytical processes” that could be performed without knowledge of the language, and “by a cryptanalyst wholly unfamiliar with the language.”54 Friedman cautioned, however, that “such a ‘solution’” may only enable the cryptanalyst to “recognize pronounceable combinations of vowels and consonants,” in effect, revealing the surface but missing the deep and meaningful structures of language.55 Therefore, the cryptanalyst invariably benefited from the further assistance of a translator. “Cooperation between cryptanalyst and translator,” wrote Friedman, “results in solution.”56
The “frequency studies” Friedman described were basically identical in kind to those first described by al-Kindi. Friedman demonstrated that across single language corpora, the “uniliteral” and “bilateral” (single and double letter) frequency distribution would remain “constant” within a “characteristic frequency” distribution, depending on the length of the text analyzed (Friedman provided charts for the expected amount of deviation in a message of a given length).57 The vowel-consonant ratio would also remain reasonably stable across an entire language.58
Statistical features of a given corpus, either ciphertext or foreign language, were critical for cryptanalysis. For pure transposition ciphers, the letter frequency distribution tables amount to a kind of signature for the text (similar to a histogram). Armed with letter frequency tables, one could visually inspect source and object letter frequencies and shift the tables by hand, lining up the crests and troughs (Fig. 2). Deviation from the expected distribution might suggest a more complex cipher, or the variance might itself be used as a guide to determine the underlying language. Similarly, echoing al-Kindi’s analysis of morphological rules, the process could be used to test for bi-, tri- or even tetragrams, such as the “rather unusual”59 succession of letters in the English word “examination.”60 Friedman cautioned that such similarities and deviations were “statistical generalizations” and may not always hold, but “nevertheless the normal frequency distribution… for any alphabetic language is… the best guide to, and the usual basis for, the solution of cryptograms of a certain type.”61
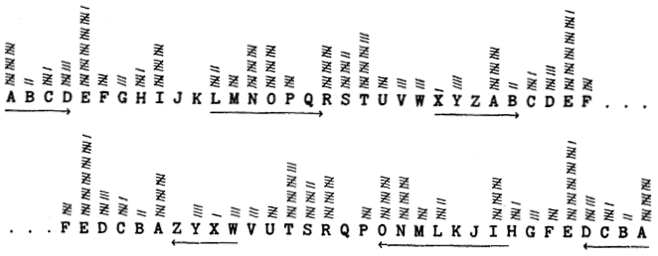
Fig. 2: Friedman’s comparison of uniliteral frequency distribution tables.62
The simple letter frequency method was an introduction to Friedman’s more complex and robust “Index of Coincidences” method, which could also be used for determining statistical features of language. For instance, the Index of Coincidences method demonstrated that a “uniliteral frequency distribution of a large volume of random text would be ‘flat,’ i.e., lacking crests and troughs,”63 yet an actual English text corpora would have a letter probability of 0.0385 – that is, a given letter would occur about 3,850 times in a corpora of 100,000 letters of English text.64 Such curves could also be determined for “other types of texts.”65 These cryptanalysis processes worked for the statistical signatures of particular languages as well, not only for corpora with different styles.
As I have argued, cryptanalysis is connected to machine translation in its methods, ontologies, and histories. This conjoined history is marked by a tension between the empiricist-statistical and rationalist-universal approaches. With respect to cryptanalysis, Friedman stressed that the cryptanalyst must draw on morphology and grammar. Yet, as a scientific method, distinguished from intuitive and craft cryptanalysis methods, his methods required measures of probabilities draw from corpora of real texts.
While Friedman was developing his cryptanalysis techniques for military personnel, electro-mechanical aids and “computers” were emerging inside and outside of the intelligence community, with promise to make quick work of the challenges faced by cryptanalysis and translation alike. Within a few decades, sophisticated cryptanalysis machines utilizing statistical techniques like those developed by Friedman had been developed, as seen by the voluminous code-breaking work during and after the Second World War.
Early Twentieth Century Machine Translation
The first two patents for machine translation were granted independently to G. Artsrouni and P. Trojanskij in 1933.66 It bears mentioning in the context of this archeology that Artsrouni’s invention would have been suitable for cryptography as he imagined it, in the sense of being able to perform encryption and decryption (but not cryptanalysis).67 That is, Artsrouni’s translation and encryption/decryption machine ultimately stemmed from an ontology and history of text processing that was distinct from that of al-Kindi and Friedman, but proximate to the work of the sixteenth and seventeenth century universal language planners.
Artsrouni believed his machine would be useful not only for translation and cryptography, but also for the automatic production of railway timetables, telephone directories, commercial telegraph codes, banking statements, and even anthropometric records (comparisons of measurements of the body). These varied uses were conceivable with Artsrouni’s device because it was simply a lookup and substitution (or permutation) machine.
The machine contained a series of bands, with each band holding the selected “content” for processing. For the translation function, the bands would hold target and source languages. To encrypt rather than translate, the bands would simply be replaced with plaintext and ciphertext versions. To use the machine for any of these possible functions, an operator would input letters on a keyboard that would cause the bands to move according to a search mechanism (the search mechanism used perforated holes in the bands and corresponding pins for selection). Once the bands matched the search criteria, the operator would compare the result displayed on the source and target bands. In this way, Artsrouni’s machine was akin to the earlier Jacquard loom or Hollerith tabulator, but Artsrouni’s machine used perforated bands in place of those machines’ perforated (or “punch”) cards. Moreover, Artsrouni’s machine functioned somewhat like Kircher’s Arca Glottotactica, as a simple mechanism for automating discrete substitutions.
For translation, comparison of the resulting bands amounted to a crude word-for-word substitution between source and target languages. Realizing the limitations for machine translation, Artsrouni advocated for the development of a universal “telegraph language” (this was less of a limitation for its encryption and decryption mode, since these techniques require only discrete permutations). This proposed telegraph language was an artificial language that had been deliberately simplified and made as unambiguous as possible.68 Using a simplified source language, it was often believed, would make word-for-word machine translation effective enough for commerce and bureaucratic communication.
Artsrouni’s machine was in fact built, at least in prototype form, and successfully demonstrated at the Paris Universal Exhibition in 1937. Orders were placed for commercial production, but the Nazi occupation of France in 1940 ended any further development or deployment. The impact of his machine is therefore limited to the annals of history, and played little to no role in the later development of machine translation.
Weaver’s “Cryptographic-Translation” Idea
Unaware of the earlier techniques and patents for machines translation, but buoyed by recent scientific and technical advances, Andrew Donald Booth and Warren Weaver met after the Second World War to discuss the possibility of machine translation. Weaver believed that soon fully-automatic, high-quality machine translation would be possible using cryptanalytic techniques developed during the War. Booth, for his part, demurred, believing it would only be possible, given the state of technology, to build a mechanical multi-lingual dictionary (akin to the designs pioneered by universal language planners and Artsrouni and Trojanskij), to be of aid to human translators.69
A major catalyst for modern machine translation research came in 1949, when Weaver, who held influential positions in American government and academic spheres, distributed a memorandum to some 200 of his colleagues (later published with the title “Translation”).70 Within just a few years, research on machine translation had a dedicated journal, international conferences, and a published collection of research essays.71
Weaver’s memorandum on machine translation started with a curious and now famous conceit.72 During the War, Weaver met an “ex-German” mathematician who had realized it was possible to cryptanalyze a message without knowing the underlying language. Moreover, Weaver also recalled that during the First World War it took American cryptanalysts longer to determine the source language of an intercepted message than it did to cryptanalyze it. To Weaver, these two facts suggested that language was really a “code,” and that to translate from one language to another, one only needed to figure out the process of decoding and recoding. Weaver wrote, “When I look at an article in Russian, I say: ‘This is really written in English, but it has been coded in some strange symbols. I will now proceed to decode.’”73 Weaver also knew that from the two wars powerful new tools for cryptanalysis were available, for example, in the form of the successful “Bombe,” Heath Robinson, and Colossus machines.
Weaver offered two descriptions of his design for the “cryptographic-translation” idea. First, he noted how the ex-German “reduced the message to a column of five digit numbers,” but was unsuccessful in deriving the plaintext because the message was still “coded” in Turkish; however, once corrected for word spacing (and some other cosmetic changes), the original Turkish was revealed.74 Again, Weaver’s point was that language was a code – it’s just that cracking natural language was tougher than cracking military ciphertext!
Second, Weaver described a method for determining the statistical semantic character of language, which he assigned a (probability) value of N. The basic value of N would change according to the language to be translated, as well as the specific genre of writing (because, he noted – echoing both al-Kindi and Friedman alike – some genres are less ambiguous than others). Thus, argued Weaver, texts would have differing probable N values, indicating their semantic character. To aid in translation, for the smallest semantic unit (the word), the value of N could also be calculated against adjacent words. Here, a particular language’s grammar would dictate that N would not always be equally distributed (i.e., “2N adjacent words”), and that there could be a distinct value for certain parts of speech (i.e., “2N adjacent nouns”).75
To the cryptanalyst of Friedman’s making, Weaver’s proposal for machine translation would seem familiar enough: cryptanalyze using n-gram divisions that have been weighted on a statistical measure of letter and word frequency analysis, combined with knowledge of grammar and morphological possibilities, and thus you have effectively performed cryptanalysis, or, for Weaver, machine translation.
This cryptanalytic process might work well for simple substitution ciphers, but Weaver realized that to do the same for two natural languages there was much less chance of success, since natural language contains a great deal of ambiguity and polysemy. Nonetheless, Weaver was confident that “processes, which at stated confidence levels will produce a translation which contains only X per cent ‘error,’ are almost surely attainable.”76 The issue at hand was, according to Weaver, “a question concerning the statistical semantic character of language.”77 The “statistical semantic character of language” that is essential to Weaver’s “cryptography-translation” idea relied on Claude Shannon’s parallel work on information and cryptology during the war.78 That is, at a basic level, Weaver believed the statistical semantic character of language was underpinned by Shannon’s information theory, the Mathematic Theory of Communication (MTC).79
Shannon himself had already made the connection between his MTC and cryptology. In fact, we can see Shannon’s thinking evolve in this direction from his publication history – from his publication of “A Mathematical Theory of Cryptography” in 1945 (in classified form),80 which detailed a logarithmic measurement of statistical information for ciphertext, to, three years later (in 1948), the publication of his famous “Mathematical Theory of Communication” article.81
Although the semantic properties of language were definitely not part of Shannon’s original MTC, Weaver extended the theory to include them in his “Recent contributions to the mathematical theory of information,” published the same year he distributed his “Translation” memorandum. In this work, Weaver stretched Shannon’s connection between cryptography and information, creating a trifecta that (confusedly) connected “cryptography” (perhaps: cryptanalysis?) to information and translation:
It is an evidence of this generality that the theory contributes importantly to, and in fact is really the basic theory of cryptography which is, of course, a form of coding. In a similar way, the theory contributes to the problem of translation from one language to another, although the complete story here clearly requires consideration of meaning, as well as of information.82 [emphasis added]
According to Weaver, the originally syntactic measurement of information that Shannon promulgated in the MTC should be augmented or replaced by semantic questions of meaning and efficacy. Here, surely, we can admit that Weaver deeply misunderstood or purposefully contorted Shannon’s theory for his own ends; but, for the purposes of understanding the connections between cryptanalysis and translation in Weaver’s proposal, his idea to use semantic information shines light on how his machine translation idea was meant to work.
Specifically, Weaver offered an amendment to Shannon’s source-receiver diagram, believing it should include a “Semantic Receiver” interposed between what he called the “engineering receiver” (Shannon’s “receiver”) and the destination (Fig. 3). Unlike Shannon’s (engineering) receiver, which only received the syntactic elements of the message, Weaver’s semantic receiver was capable of receiving semantic elements, and also attempted to match these semantics to those in the “totality of receivers.”83 In other words, the meaning of the message was to be compared to the meanings of all possible messages.
Fig. 3: Shannon’s model of communication.84
Weaver admitted that these alterations to Shannon’s MTC must have seemed “disappointing and bizarre,” as though he understood that he had confused Shannon’s otherwise clear concept.85 These changes are less disappointing and bizarre, however, when we realize that all along Weaver clearly had in the back of his mind the “cryptographic-translation idea,” hatched in the very same year, and which required the use of statistical semantics because, as any good cryptanalyst after Friedman knows, the statistical “semantics” of natural language are not evenly distributed, and therefore can be exploited to one’s cryptanalytic or translation advantage.
In fact, the history of cryptology is full of codes cracked because statistical semantics were utilized in cryptanalysis. For example, this approach can be used to attack a weak cipher when used on repetitive, common, or “probable” words (in the vein of al-Kindi or Friedman), such as in the opening salutations of epistolary letters, or certain stylistic rhetorical devices. The supposed weakness of Shannon’s information theory, identified by Weaver, is that it has nothing to say about the fact that “Hello ____” is more likely to turn out to be “Hello Dolly” than it is “Hello running” (or “Hello hY!DSh;sf”).86 This fact – the way real words are ordered in real use, and not just the data points of “information” – is critical and often decisive for the cryptanalyst.87 Likewise, a translator (machine or human) could (and should) leverage this information, since a specific language’s grammar only permits certain orderings of words for the construction of meaningful articulations. This technical advantage explains why Weaver concluded his machine translation memorandum with a request that “statistical semantic studies should be undertaken, as a necessary preliminary step.”88
Machine Translation after Weaver
Research on machine translation continued after Weaver. In the 1960s, Bar-Hillel produced an influential survey of the field of machine translation and concluded not only that the prospect of fully-automatic high-quality translation was unrealistic given the current state of technology, but that the entire project was impossible in principle.89 Government sponsors grew skeptical of machine translation research and worried about its slow progress, as expressed in the Automatic Language Processing Advisory Committee report issued in 1964. Pre- and post- editing machine translation by humans was the norm, which required considerable time and effort.
By the 1980s, however, fully-automatic high-quality machine translation was finally a reality, and starting to find significant use within governments and private organizations. New methods and models improved the quality of translation, and the introduction of faster and cheaper microcomputers spurred further success while continuing to drive costs down. In the 1990s, research significantly moved away from rationalist approaches that had sought to understand underlying linguistic rules across source and target languages, and instead used large language corpora and sophisticated statistics.
Following this trend, in recent years Google has emerged as a leader in the field, with its ability to leverage vast stores of data collected from the web and across its personalized services, in conjunction with its expertise in algorithmic data processing and machine learning. However, Google’s approach to machine translation has, perhaps decisively, severed the existing tension between rationalist and empiricist approaches, which had co-existed in the histories of machine translation and cryptanalysis since its earliest days. In fact, Google openly declares that they do not employ linguists,90 and has even created inter-language dictionaries programmatically, without relying on the intuitions of humans or underlying linguistic rules.91 Their approach has been, arguably, quite successful, and mirrors trends in modern cryptanalysis too (which long ago became too complex for human hands). Today, machine translation and cryptanalysis has little role for linguists or rational models of language. “Number crunching,” for machine translation and cryptanalysis both, is now the norm.
Friedrich Kittler, Gramophone, Film, Typewriter, trans. Geoffrey Winthrop-Young and Michael Wutz, 1st edition (Stanford, CA: Stanford University Press, 1999). ↩
Guy Podjarny, “HTTPS Adoption *doubled* This Year,” Snyk, July 20, 2016, https://snyk.io/blog/https-breaking-through/; Klint Finley, “It’s Time to Encrypt the Entire Internet,” Wired, accessed November 12, 2014, http://www.wired.com/2014/04/https/. ↩
Encryption is a process of mereology, order, and reference, where atomic inscriptions (“notations”) are “semantically” denoted by other atomic inscriptions. For an in-depth exploration of encryption/decryption, see Quinn DuPont, “An Archeology of Cryptography: Rewriting Plaintext, Encryption, and Ciphertext” (PhD diss., University of Toronto, 2016). ↩
W. John Hutchins, “Machine Translation: History,” Encyclopedia of Language and Linguistics (San Diego, CA: Elsevier Science & Technology Books, 2006). ↩
W. John Hutchins, “Two Precursors of Machine Translation: Artsrouni and Trojanskij,” International Journal of Translation 16, no. 1 (2004): 11–31. ↩
Rita Raley, “Machine Translation and Global English,” The Yale Journal of Criticism 16, no. 2 (2003): 291–313, doi:10.1353/yale.2003.0022. ↩
Christine Mitchell, “Situation Normal, All FAHQT Up: Language, Materiality & Machine Translation” (PhD diss., McGill University, 2010). ↩
David Kahn, The Codebreakers, Abridged (London: Sphere Books Limited, 1977), 80. ↩
Not all scholars in this milieu wrote or spoke in Arabic, but most did, since, according to Chase F. Robinson, Arabic was considered the “prestige language of scholarship.” In fact, there is no good catch-all term to denote the peoples involved in this intellectually and politically vibrant climate. Many languages were spoken and written, many cultures and races were actively participating, many religions were represented, and the geography was vast. For these reasons, I use the accepted terminology of “Arabic” scholar, rather than “Arab” or “Muslim.” See Chase F. Robinson, Islamic Historiography (New York: Cambridge University Press, 2003). ↩
It has also been argued that papermaking skills (also necessary for state administration) were an important factor in the development of Arabic cryptology, see Kathryn A. Schwartz, “From Text to Technological Context: Medieval Arabic Cryptology’s Relation to Paper, Numbers, and the Post,” Cryptologia 38, no. 2 (April 3, 2014): 133–46. ↩
Dimitri Gutas, Greek Thought, Arabic Culture: The Graeco-Arabic Translation Movement in Baghdad and Early ʻAbbāsid Society (2nd-4th/8th-10th Centuries) (New York: Routledge, 1998). ↩
See, for instance, Peter Pesic, Labyrinth: A Search for the Hidden Meaning of Science (Cambridge, Mass.: MIT Press, 2000). ↩
Miriam Cooke, “Ibn Khaldun and Language: From Linguistic Habit to Philological Craft,” Journal of Asian and African Studies 18, no. 3–4 (January 1, 1983): 179–88. ↩
Umberto Eco, The Search for the Perfect Language, trans. James Fentress (Cambridge, Mass., USA: Blackwell, 1995). ↩
Cooke, “Ibn Khaldun and Language.” ↩
These first works were edited and published in Arabic in 1989 by a group of scholars in Damascus. Since 2003 they have re-published the earliest works in a new series, alongside other recently discovered works, now totalling six volumes available in edited Arabic versions with English translation. See Ibrahim A. Al-Kadi, “Origins of Cryptology: The Arab Contributions,” Cryptologia 16, no. 2 (1992): 97–126, doi:10.1080/0161-119291866801; Kathryn A. Schwartz, “Charting Arabic Cryptology’s Evolution,” Cryptologia 33, no. 4 (2009): 297–304, doi:10.1080/01611190903030904; Schwartz, “From Text to Technological Context.” ↩
Al-Kindi’s work is now the oldest extant work on cryptography and cryptanalysis, although there are references to even earlier Arabic works, dating to the early eighth century. Mohammed Mrayati, Meer Alam Yahya, and at-Tayyan Hassan, eds., Al-Kindi’s Treatise of Cryptanalysis, trans. Said M. al-Asaad, The Arabic Origins of Cryptology 1 (Riyadh: KFCRIS & KACST, 2003). ↩
Giovanni Battista Alberti, “De Componendis Cifris,” in The Mathematical Works of Leon Battista Alberti, ed. Kim Williams, Lionel March, and Stephen R. Wassell (Basel: Springer Basel, 2010), 169–87, https://link.springer.com/chapter/10.1007/978-3-0346-0474-1_4. See also Quinn DuPont, “The Printing Press and Cryptography: Alberti and the Dawn of a Notational Epoch,” in A Material History of Medieval and Early Modern Ciphers: Cryptography and the History of Literacy, ed. Katherine Ellison and Susan Kim, Material Readings in Early Modern Culture (New York: Routledge, 2017). ↩
The English term “cipher” originates from a Latin version of the Arabic sifr, meaning zero. See Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 24. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 24–32. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 24. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 122. ↩
Al-Kindi was, it seems, implicitly aware of the differences between letter frequency distributions in various genres or styles, but he never discusses it. It was Alberti, in his De Componendis Cifris (1467), who made the first ever explicit “stylometric” observations. See Alberti, “De Componendis Cifris”; Bernard Ycart, “Letter Counting: A Stem Cell for Cryptology, Quantitative Linguistics, and Statistics,” Historiographia Linguistica 40, no. 3 (2013): 303–30, doi:10.1075/hl.40.3.01yca; Bernard Ycart, “Alberti’s Letter Counts,” Literary and Linguistic Computing 29, no. 2 (June 1, 2014): 255–65, doi:10.1093/llc/fqt034. ↩
Ycart, “Letter Counting,” 314. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 122. ↩
The first Western cryptology manual to give letter frequency tables was Charles François Vesin de Romanini in the mid-nineteenth century. The practice of producing and using letter frequency tables was considered by Babbage and Quetelet to be one of the “constants of nature and arts,” and of critical value to printers who would need to ensure sufficient quantities of metal type were ordered. Samuel Morse utilized the letter frequency values of printer’s cases when determining compression efficiencies for his binary telegraph code. See Ycart, “Letter Counting,” 307, 312. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 123. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 168. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 172 ff. ↩
Mohammed Mrayati, Meer Alam Yahya, and at-Tayyan Hassan, eds., Ibn `Adlan’s Treatise Al-Mu’allaf Lil-Malik Al’Asraf, trans. Said M. al-Asaad, The Arabic Origins of Cryptology 2 (Riyadh: KFCRIS & KACST, 2005). ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 128. ↩
Mrayati, Yahya, and Hassan, Al-Kindi’s Treatise of Cryptanalysis, 128. ↩
DuPont, “The Printing Press and Cryptography: Alberti and the Dawn of a Notational Epoch.” ↩
Gary Genosko, “Regaining Weaver and Shannon,” The Fiberculture Journal 12 (2008), http://twelve.fibreculturejournal.org/fcj-079-regaining-weaver-and-shannon/; Brian Lennon, In Babel’s Shadow : Multilingual Literatures, Monolingual States (Minneapolis, US: University of Minnesota Press, 2010), 62, http://site.ebrary.com/lib/alltitles/docDetail.action?docID=10399440 ff. ↩
Eco, The Search for the Perfect Language; Jaap Maat, Philosophical Languages in the Seventeenth Century: Dalgarno, Wilkins, Leibniz (Dordrecht: Springer, 2004); Mary M. Slaughter, Universal Languages and Scientific Taxonomy in the Seventeenth Century (Cambridge: Cambridge University Press, 2010). ↩
This tradition has many conceptual connections to machine translation, pace Hutchins, a leading historian of machine translation. Hutchins argues that the universal language planners did not contribute to contemporary machine translation in a meaningful way, writing “these [universal language] proposals must not be considered in any way as constituting embryonic automatic translation systems.” Despite his dismissal of the connection, Hutchins also includes several accounts of the translation activities of universal language planners. See W. John Hutchins, “Two Precursors of Machine Translation: Artsrouni and Trojanskij,” International Journal of Translation 16, no. 1 (2004): 11–31. ↩
See Daniel Stolzenberg, ed., The Great Art of Knowing: The Baroque Encyclopedia of Athanasius Kircher (Florence, Italy: Stanford University Libraries, 2001). ↩
The earlier “Arca Musarithmica” is described in Musurgia Universalis, but Kircher’s more ambitious “Organum Mathematicum,” which includes music as one of many possible topics, is extant only in Gaspar Schott’s Schola Steganographica and a few prototypes. ↩
George E. McCracken, “Athanasius Kircher’s Universal Polygraphy,” Isis 39, no. 4 (November 1, 1948): 215–28. ↩
Hutchins, “Two Precursors of Machine Translation.” ↩
Wayne Shumaker, Renaissance Curiosa: John Dee’s Conversations with Angels, Girolamo Cardano’s Horoscope of Christ, Johannes Trithemius and Cryptography, George Dalgarno’s Universal Language, Medieval & Renaissance Texts & Studies 8 (Binghamton, NY: Center for Medieval & Early Renaissance Studies, 1982), 139, 193. ↩
See editor’s introduction in John Wilkins, Mercury: Or, The Secret and Swift Messenger. Shewing, How a Man May with Privacy and Speed Communicate His Thoughts to a Friend at Any Distance. Reprinted from the Third Edition (1708), Foundations of Semiotics 6 (Amsterdam; Philadelphia: John Benjamins Publishing Company, 1984), xlv. ↩
Pesic, Labyrinth. ↩
This transition between “manual” and “automated” or “computing” technologies was far from instant. Matthew Jones argues that the prior simply “complimented” the latter, well into the twentieth century. Matthew L. Jones, “Calculating Devices and Computers,” in A Companion to the History of Science, ed. Bernard V. Lightman, Blackwell Companions to World History (Malden, MA: John Wiley & Sons, 2016), 472–81. ↩
Nicholas Rescher, “Leibniz’s Machina Deciphratoria: A Seventeenth-Century Proto-Enigma,” Cryptologia 38, no. 2 (April 3, 2014): 103–15. ↩
Friedman became chief cryptologist in 1952, at the formation of the NSA. ↩
Later republished as William F. Friedman, The Index of Coincidence and Its Applications in Cryptanalysis, A Cryptographic Series 49 (Laguna Hills, CA: Aegean Park Press, 1987). ↩
Kahn, The Codebreakers, 167. ↩
For a description of the cutting edge of cryptanalysis at this time, see Whitfield Diffie, James A. Reeds, and J. V. Field, Breaking Teleprinter Ciphers at Bletchley Park: An Edition of I.J. Good, D. Michie and G. Timms: General Report on Tunny with Emphasis on Statistical Methods (1945) (John Wiley & Sons, 2015). ↩
William F. Friedman, Military Cryptanalysis: Part I Monoalphabetic Substitution Systems (Washington, DC: United States Government Printing Office, 1938), 7. ↩
Friedman, Military Cryptanalysis: Part I, 7. ↩
Friedman, Military Cryptanalysis: Part I, 8. ↩
Friedman, Military Cryptanalysis: Part I, 8. ↩
Friedman, Military Cryptanalysis: Part I, 8. ↩
Friedman, Military Cryptanalysis: Part I, 8. ↩
Friedman, Military Cryptanalysis: Part I, 8. ↩
Friedman, Military Cryptanalysis: Part I, 12, 20. ↩
Friedman, Military Cryptanalysis: Part I , 14. ↩
Friedman, Military Cryptanalysis: Part I, 54. ↩
Friedman, Military Cryptanalysis: Part I, 49. ↩
Friedman, Military Cryptanalysis: Part I, 16. ↩
Friedman, Military Cryptanalysis: Part I, 28. ↩
Friedman, Military Cryptanalysis: Part II, 108. ↩
Friedman, Military Cryptanalysis: Part II, 109. ↩
Friedman, Military Cryptanalysis: Part II, 112. ↩
There is also some indication that some unknown experimenters tried to produce typewriter-translators in the early twentieth century. See Hutchins, “Two Precursors of Machine Translation.” ↩
Hutchins, “Two Precursors of Machine Translation.” ↩
For comparison with Weaver’s later suggestion to use Basic English for translation, see Raley, “Machine Translation and Global English.” ↩
A year after Booth and Weaver’s first tentative discussions, Booth and Richens worked out a “code” for mechanized dictionary translation, detailed in a Rockefeller Foundation report in 1947. See William N. Locke and A. Donald Booth, eds., Machine Translation of Languages (New York: The Technology Press of The Massachusetts Institute of Technology, 1955), 3. ↩
Warren Weaver, “Translation,” in Machine Translation of Languages, ed. William Nash Locke and Andrew Donald Booth (Technology Press of Massachusetts Institute of Technology, 1955). ↩
Locke and Booth, Machine Translation of Languages. ↩
See also Christine Mitchell, “Unweaving Weaver from Contemporary Critiques of Machine Translation” (Canadian Association of Translation Studies Annual Conference at Carleton University, Ottawa, ON, 2009), http://act-cats.ca/wp-content/uploads/2015/04/Mitchell_Unweaving-Weaver.pdf. ↩
Weaver, “Translation,” 18. ↩
Weaver, “Translation,” 16. ↩
Weaver, “Translation,” 21. ↩
Weaver, “Translation,” 22. ↩
Weaver, “Translation,” 21. ↩
See also Genosko, “Regaining Weaver and Shannon.” ↩
Warren Weaver, “Recent Contributions to the Mathematical Theory of Communication,” The Mathematical Theory of Communication, 1949, 93–117. ↩
Claude Shannon, “A Mathematical Theory of Cryptography” (Murray Hill, NJ: Bell Labs, September 1, 1945), http://www.cs.bell-labs.com/who/dmr/pdfs/shannoncryptshrt.pdf. ↩
Claude Shannon and Warren Weaver, “A Mathematical Theory of Communication,” Bell System Technical Journal 27 (1948): 379–423. ↩
Weaver, “Recent Contributions to the Mathematical Theory of Communication,” 14. ↩
Weaver, “Recent Contributions,” 15. ↩
Weaver, “Recent Contributions,” 4. ↩
Weaver, “Recent Contributions,” 15. ↩
Part of the reason for this fact is that the statistical measure in the MTC – entropy – is measured at the level of the smallest unit (usually a bit), not at the level of word, sentence, or larger semantic divisions. ↩
This method of cryptanalysis is now largely useless, in the age of massively entropic encryption algorithms, however, prior to the advent of software encryption (in the 1960s), the “probable” word method would have still been useful. For the history of early software encryption systems, see Jeffrey R. Yost, “The Origin and Early History of the Computer Security Software Products Industry,” IEEE Annals of the History of Computing 37, no. 2 (April 2015): 46–58, doi:10.1109/MAHC.2015.21; Quinn DuPont and Bradley Fidler, “Edge Cryptography and the Co-Development of Computer Networks and Cybersecurity,” IEEE Annals of the History of Computing 38, no. 2 (2016): 55–73, doi:10.1109/MAHC.2016.49. ↩
Weaver, “Translation,” 11. ↩
Hutchins, “Machine Translation: History,” 375. ↩
Thomas Schulz, “Translate This: Google’s Quest to End the Language Barrier,” Spiegel Online, September 13, 2013, sec. International, http://www.spiegel.de/international/europe/google-translate-has-ambitious-goals-for-machine-translation-a-921646.html. ↩
Nataly Kelly, “Why Machines Alone Cannot Solve the World’s Translation Problem,” Smartling, January 9, 2014, https://www.smartling.com/2014/01/09/machines-solve-worlds-translation-problem/. ↩
Article: Creative Commons Attribution-Non-Commercial 3.0 Unported License.